Memahami Matematika: Panduan Lengkap Konsep Dasar |

Memahami Matematika: Panduan Lengkap Konsep Dasar – Halo, Adik-adik dan para pelajar di seluruh Indonesia! Pernahkah kalian merasa takut atau pusing saat mendengar kata “matematika”? Kalian tidak sendirian, kok! Banyak orang menganggap matematika sebagai mata pelajaran yang sulit dan penuh dengan rumus-rumus rumit. Padahal, jika kita mau sedikit bersabar dan memahami konsep dasar matematika dengan benar, matematika itu justru bisa menjadi mata pelajaran yang sangat menyenangkan dan logis.

Table of Contents

Sama seperti membangun sebuah rumah, kita tidak bisa langsung memasang atap tanpa membuat fondasi yang kuat. Begitu juga dengan matematika. Fondasi yang kokoh akan membuat kalian lebih mudah untuk menguasai materi yang lebih kompleks. Artikel ini akan menjadi panduan lengkap kalian untuk memahami kembali fondasi-fondasi penting dalam matematika, dari yang paling dasar hingga yang mungkin belum pernah kalian kenal sebelumnya. Kita akan membahasnya dengan bahasa yang santai, langkah demi langkah, dan tentunya dengan banyak contoh yang mudah dipahami. Yuk, kita bangun fondasi matematika kita bersama-sama!

Bagian 1: Mengenal Dunia Bilangan

Segala sesuatu dalam matematika dimulai dari bilangan. Tanpa bilangan, kita tidak bisa menghitung, mengukur, atau bahkan berinteraksi dengan dunia di sekitar kita. Penting untuk membedakan antara angka dan bilangan. Angka adalah simbol yang kita gunakan (seperti 0, 1, 2, 3, 4, 5, 6, 7, 8, 9), sedangkan bilangan adalah nilai yang terbentuk dari angka-angka tersebut (seperti 10, 25, 100).

Dalam matematika, ada beberapa jenis bilangan yang harus kalian kenal:

Bilangan Bulat: Bilangan yang terdiri dari bilangan cacah dan bilangan negatifnya. Contohnya: …, $- 3, - 2, - 1, 0, 1, 2, 3, \dots$ .
Bilangan Pecahan: Bilangan yang mewakili bagian dari keseluruhan, ditulis dalam bentuk $b a$ . Di mana $a$ adalah pembilang dan $b$ adalah penyebut. Contohnya: $2 1, 4 3, 8 5$ .
Bilangan Desimal: Bilangan yang memiliki tanda koma. Bilangan ini sebenarnya adalah bentuk lain dari pecahan dengan penyebut 10, 100, 1000, dan seterusnya. Contohnya: $0, 5$ (sama dengan $2 1$ ), $0, 75$ (sama dengan $4 3$ ).
Bilangan Rasional: Bilangan yang dapat dinyatakan dalam bentuk pecahan $b a$ , di mana $a$ dan $b$ adalah bilangan bulat dan $b \neq = 0$ . Semua bilangan bulat, pecahan, dan desimal terbatas (seperti $0, 25$ ) adalah bilangan rasional.
Bilangan Irasional: Bilangan yang tidak dapat dinyatakan dalam bentuk pecahan. Bilangan ini memiliki deretan angka di belakang koma yang tidak berulang dan tidak berhenti. Contoh yang paling terkenal adalah $π$ (pi, yang nilainya sekitar 3,14159…) dan $2$ (akar kuadrat dari 2, yang nilainya sekitar 1,41421…).

Setelah mengenal jenis-jenis bilangan, kalian juga harus menguasai operasi dasar matematika: penjumlahan (+), pengurangan (-), perkalian (x), dan pembagian (:). Ingatlah aturan “urutan operasi” atau yang biasa disingkat “PEMDAS” (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) atau “KU-KA-LI-BA-TA-KU” (Kurung, Kali, Bagi, Tambah, Kurang). Aturan ini memastikan hasil perhitungan kalian selalu benar.

Bagian 2: Aljabar – Matematika dengan Huruf

Mungkin ini adalah salah satu materi yang paling ditakuti. Mengapa tiba-tiba ada huruf (seperti $x$ dan $y$ ) di dalam matematika? Jangan khawatir! Dalam aljabar, huruf-huruf ini disebut variabel yang berfungsi sebagai “tempat penampung” untuk sebuah nilai yang belum diketahui. Aljabar adalah bagian dari matematika yang menggunakan simbol dan huruf untuk mewakili bilangan dan hubungan antar bilangan.

Ekspresi Aljabar: Sebuah kombinasi dari variabel, angka, dan operasi matematika. Contohnya: $5 x + 2$ . Di sini, $x$ adalah variabel, $5$ adalah koefisien (angka yang menempel pada variabel), dan $2$ adalah konstanta (angka yang tidak berubah).
Persamaan Aljabar: Sebuah pernyataan matematika yang menunjukkan bahwa dua ekspresi aljabar memiliki nilai yang sama, ditandai dengan tanda sama dengan (=). Contohnya: $2 x + 5 = 11$ .

Tujuan utama dalam aljabar adalah menemukan nilai variabel yang membuat persamaan itu benar. Misalnya, untuk menyelesaikan $2 x + 5 = 11$ , kita bisa menggunakan langkah-langkah berikut:

Kurangi kedua sisi dengan 5: $2 x + 5 - 5 = 11 - 5 \to 2 x = 6$ .
Bagi kedua sisi dengan 2: $2 2 x = 2 6 \to x = 3$ . Jadi, nilai $x$ yang memenuhi persamaan tersebut adalah 3.

Selain itu, kalian juga akan belajar faktorisasi aljabar. Faktorisasi adalah proses memecah ekspresi aljabar menjadi faktor-faktornya. Contohnya, ekspresi $x^{2} - 4$ bisa difaktorkan menjadi $(x - 2) (x + 2)$ . Kemampuan faktorisasi ini sangat penting untuk menyelesaikan banyak soal, terutama di materi limit fungsi aljabar yang sudah kalian kenal sebelumnya.

Bagian 3: Geometri – Matematika dalam Bentuk dan Ruang

Geometri adalah cabang matematika yang mempelajari tentang bentuk, ukuran, posisi, dan sifat-sifat ruang. Dari bentuk yang paling sederhana hingga yang paling kompleks, semuanya dipelajari dalam geometri.

A. Bangun Datar

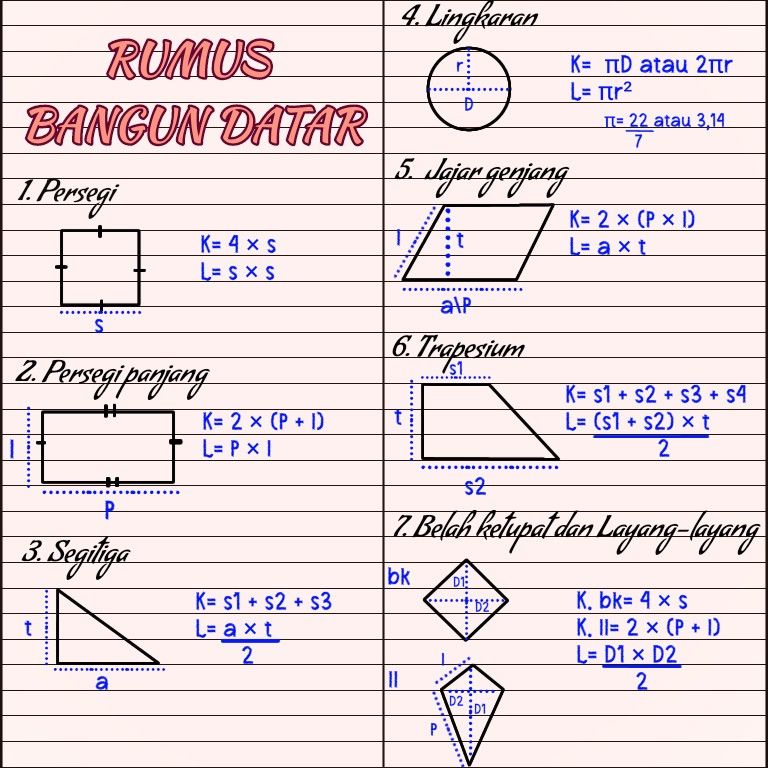
Bangun datar adalah objek dua dimensi yang hanya memiliki panjang dan lebar. Beberapa yang paling umum adalah:

Persegi: Memiliki empat sisi sama panjang dan empat sudut 90 derajat. Luasnya adalah sisi x sisi ( $s^{2}$ ) dan kelilingnya adalah $4 \times s$ .
Persegi Panjang: Memiliki dua pasang sisi yang sama panjang dan empat sudut 90 derajat. Luasnya adalah panjang x lebar ( $p \times l$ ) dan kelilingnya adalah $2 \times (p + l)$ .
Segitiga: Memiliki tiga sisi. Luasnya adalah $2 1 \times alas \times tinggi$ . Kelilingnya adalah jumlah panjang ketiga sisinya.
Lingkaran: Memiliki satu sisi melengkung. Luasnya adalah $π r^{2}$ dan kelilingnya adalah $2 π r$ .

B. Bangun Ruang

Bangun ruang adalah objek tiga dimensi yang memiliki panjang, lebar, dan tinggi.

Kubus: Memiliki enam sisi yang berbentuk persegi. Volumenya adalah $s \times s \times s$ ( $s^{3}$ ) dan luas permukaannya adalah $6 \times s^{2}$ .
Balok: Memiliki enam sisi, di mana sisi-sisi yang berhadapan sama. Volumenya adalah $p \times l \times t$ dan luas permukaannya adalah $2 (pl + pt + lt)$ .
Tabung: Memiliki dua sisi alas dan tutup berbentuk lingkaran dan satu sisi selimut melengkung. Volumenya adalah $π r^{2} t$ .

C. Transformasi Geometri

Ini adalah materi yang mempelajari perubahan posisi dan bentuk suatu objek.

Translasi (Pergeseran): Memindahkan objek tanpa mengubah bentuk dan ukurannya.
Refleksi (Pencerminan): Mencerminkan objek pada suatu garis atau sumbu.
Rotasi (Perputaran): Memutar objek di sekitar suatu titik.

Bagian 4: Statistika – Mengolah Data untuk Mengambil Keputusan

Dalam dunia yang penuh dengan informasi, statistika adalah ilmu yang sangat penting. Statistika adalah ilmu yang mempelajari cara mengumpulkan, mengolah, menganalisis, dan menyajikan data. Tujuannya adalah untuk menarik kesimpulan yang valid dan membuat keputusan yang tepat.

Beberapa konsep dasar dalam statistika adalah:

Data: Kumpulan informasi atau fakta. Data bisa berupa angka (misalnya, nilai ujian) atau kualitatif (misalnya, warna favorit).
Populasi: Seluruh objek yang menjadi target pengamatan.
Sampel: Sebagian kecil dari populasi yang diambil untuk dianalisis, yang dianggap mewakili populasi.

Kita juga akan belajar tentang ukuran pemusatan data, yang digunakan untuk menggambarkan nilai “pusat” dari suatu data.

Mean (Rata-rata): Jumlah semua nilai data dibagi dengan banyaknya data. Ini adalah ukuran yang paling sering digunakan.
Median (Nilai Tengah): Nilai yang berada di tengah-tengah setelah data diurutkan dari yang terkecil ke yang terbesar.
Modus: Nilai yang paling sering muncul dalam suatu data.

Bagian 5: Peluang – Mengukur Kemungkinan

Pernahkah kalian melempar koin dan bertanya-tanya, “Apakah akan muncul gambar atau angka?” Pertanyaan ini dijawab oleh ilmu peluang. Peluang adalah ilmu yang mempelajari kemungkinan terjadinya suatu peristiwa.

Ruang Sampel: Himpunan semua kemungkinan hasil dari suatu percobaan. Misalnya, ruang sampel saat melempar sebuah dadu adalah ${1, 2, 3, 4, 5, 6}$ .
Titik Sampel: Satu kemungkinan hasil dalam ruang sampel. Contohnya, angka 4 adalah salah satu titik sampel dari pelemparan dadu.
Rumus Peluang: Peluang suatu kejadian $A$ terjadi dihitung dengan rumus:
$P (A) = Banyaknya ruang sampel Banyaknya kejadian A$ Contoh: Peluang munculnya angka 2 saat melempar sebuah dadu adalah $6 1$ karena hanya ada satu angka 2 dari enam kemungkinan hasil.

Kesimpulan

Adik-adik, kalian telah berhasil menelusuri rangkuman lengkap dari konsep-konsep dasar matematika. Kalian sekarang tahu bahwa matematika bukan hanya tentang angka-angka, tetapi juga tentang hubungan, bentuk, data, dan kemungkinan. Dengan memahami bilangan, aljabar, geometri, statistika, dan peluang, kalian telah membangun fondasi yang kokoh.

Kunci untuk menguasai semua materi ini adalah latihan secara rutin. Matematika adalah keterampilan, dan seperti keterampilan lainnya, semakin sering kalian berlatih, semakin mahir kalian. Jangan ragu untuk mencoba berbagai jenis soal dan mencari bantuan jika kalian menemui kesulitan. Dengan pola pikir yang benar dan semangat yang tidak pernah menyerah, kalian pasti bisa menjadi jagoan matematika. Selamat belajar dan terus semangat!

10 Kuis dari Artikel:

Jelaskan perbedaan antara angka dan bilangan!
Bilangan seperti apakah yang termasuk dalam kategori bilangan irasional?
Dalam ekspresi aljabar $7 x + 3$ , manakah yang disebut koefisien dan manakah yang disebut konstanta?
Jika sebuah segitiga memiliki alas $10$ cm dan tinggi $6$ cm, berapakah luasnya?
Sebutkan tiga jenis transformasi geometri yang disebutkan dalam artikel!
Apa yang dimaksud dengan mean dalam statistika?
Dalam sebuah data, apa yang dimaksud dengan modus?
Sebutkan perbedaan antara populasi dan sampel dalam statistika!
Apa yang dimaksud dengan ruang sampel dalam peluang?
Berapakah peluang munculnya angka genap saat melempar sebuah dadu?

Jangan Ketinggalan Info Pendidikan Terbaru!

Yuk, gabung sekarang di Channel WhatsApp INFO Pendidikan kami untuk mendapatkan update terkini seputar dunia pendidikan, termasuk informasi penting mengenai materi pelajaran, tips belajar, dan banyak lagi!

KLIK DI SINI UNTUK GABUNG: https://whatsapp.com/channel/0029VaoZFfj1Hspp1XrPnP3q

Dapatkan Update Pendidikan Langsung di Telegram!

Temukan berbagai informasi penting seputar dunia pendidikan, mulai dari tips belajar efektif, materi sekolah, hingga info beasiswa, di Channel Telegram INFO Pendidikan.

KLIK DI SINI UNTUK GABUNG: https://t.me/Infopendidikannew