Logaritma: Memahami Konsep, Aturan, dan Penerapannya dalam Kehidupan Sehari-hari |

Logaritma: Memahami Konsep, Aturan, dan Penerapannya dalam Kehidupan Sehari-hari – Pengantar: Membongkar Misteri Logaritma. Pernahkah kamu mendengar kata “logaritma”? Bagi sebagian pelajar, kata ini mungkin terdengar asing atau bahkan menakutkan. Namun, jangan khawatir! Pada dasarnya, logaritma bukanlah hal yang rumit. Ia hanyalah sebuah konsep matematika yang berfungsi sebagai kebalikan dari eksponen. Jika eksponen bertanya, “Berapa hasil dari 10 dipangkatkan 2?”, maka logaritma bertanya, “Berapa pangkat yang dibutuhkan untuk mengubah 10 menjadi 100?”. Sederhana, bukan?

Table of Contents

Dalam artikel ini, kita akan bersama-sama menjelajahi dunia logaritma. Kita akan membedah definisi dasarnya, memahami cara membacanya, dan mengupas tuntas berbagai operasi dan properti yang melekat padanya. Tak hanya itu, kita juga akan melihat bagaimana logaritma, yang seringkali dianggap abstrak, ternyata memiliki peran penting dalam berbagai bidang ilmu dan bahkan dalam kehidupan kita sehari-hari.

Memahami Esensi Logaritma: Definisi dan Notasi

Secara formal, logaritma adalah operasi matematika yang merupakan invers dari eksponensiasi. Dengan kata lain, ia adalah cara lain untuk menyatakan sebuah hubungan pangkat. Jika kita memiliki persamaan eksponensial $b^{y} = x$ , maka bentuk logaritmanya adalah $log_{b} (x) = y$ . Mari kita pecah satu per satu:

$b$ adalah basis atau bilangan pokok. Ini adalah angka yang akan dipangkatkan.
$x$ adalah numerus atau argumen logaritma. Ini adalah hasil dari perpangkatan.
$y$ adalah hasil logaritma atau eksponen. Ini adalah pangkat yang kita cari.

Untuk mempermudah, bayangkan sebuah “logaritma” sebagai “pencari pangkat”. Ia bertugas mencari tahu pangkat berapa yang harus kita berikan pada sebuah basis agar menghasilkan numerus tertentu. Sebagai contoh, perhatikan persamaan $1 0^{2} = 100$ . Dalam bentuk logaritma, persamaan ini ditulis sebagai $log_{10} (100) = 2$ . Bacanya, “logaritma 100 dengan basis 10 adalah 2”. Ini berarti, untuk mendapatkan 100, kita harus memangkatkan 10 sebanyak 2 kali.

Notasi logaritma yang paling umum adalah “log”. Jika basis tidak ditulis, biasanya diasumsikan basisnya adalah 10. Misalnya, $log (100) = 2$ sama artinya dengan $log_{10} (100) = 2$ . Ada juga logaritma natural yang basisnya adalah bilangan Euler ( $e \approx 2.71828\dots$ ). Logaritma natural ini disimbolkan dengan “ln”. Jadi, $ln (x)$ sama dengan $log_{e} (x)$ .

Mengapa Logaritma Begitu Penting?

Mungkin kamu bertanya, “Untuk apa sih repot-repot belajar logaritma kalau sudah ada eksponen?”. Pertanyaan ini sangat wajar. Logaritma memiliki beberapa kegunaan fundamental yang menjadikannya alat yang sangat ampuh dalam berbagai disiplin ilmu:

1. Menyederhanakan Perhitungan yang Kompleks

Logaritma dapat mengubah operasi perkalian dan pembagian yang rumit menjadi operasi penjumlahan dan pengurangan yang lebih sederhana. Ini sangat berguna dalam perhitungan manual, terutama sebelum era kalkulator. Contohnya, untuk menghitung $1000 \times 100$ , kita bisa menggunakan logaritma. $log (1000 \times 100) = log (1000) + log (100) = 3 + 2 = 5$ . Hasil logaritma ini, 5, adalah pangkat dari 10. Jadi, $1 0^{5} = 100.000$ .

2. Merepresentasikan Skala yang Sangat Besar

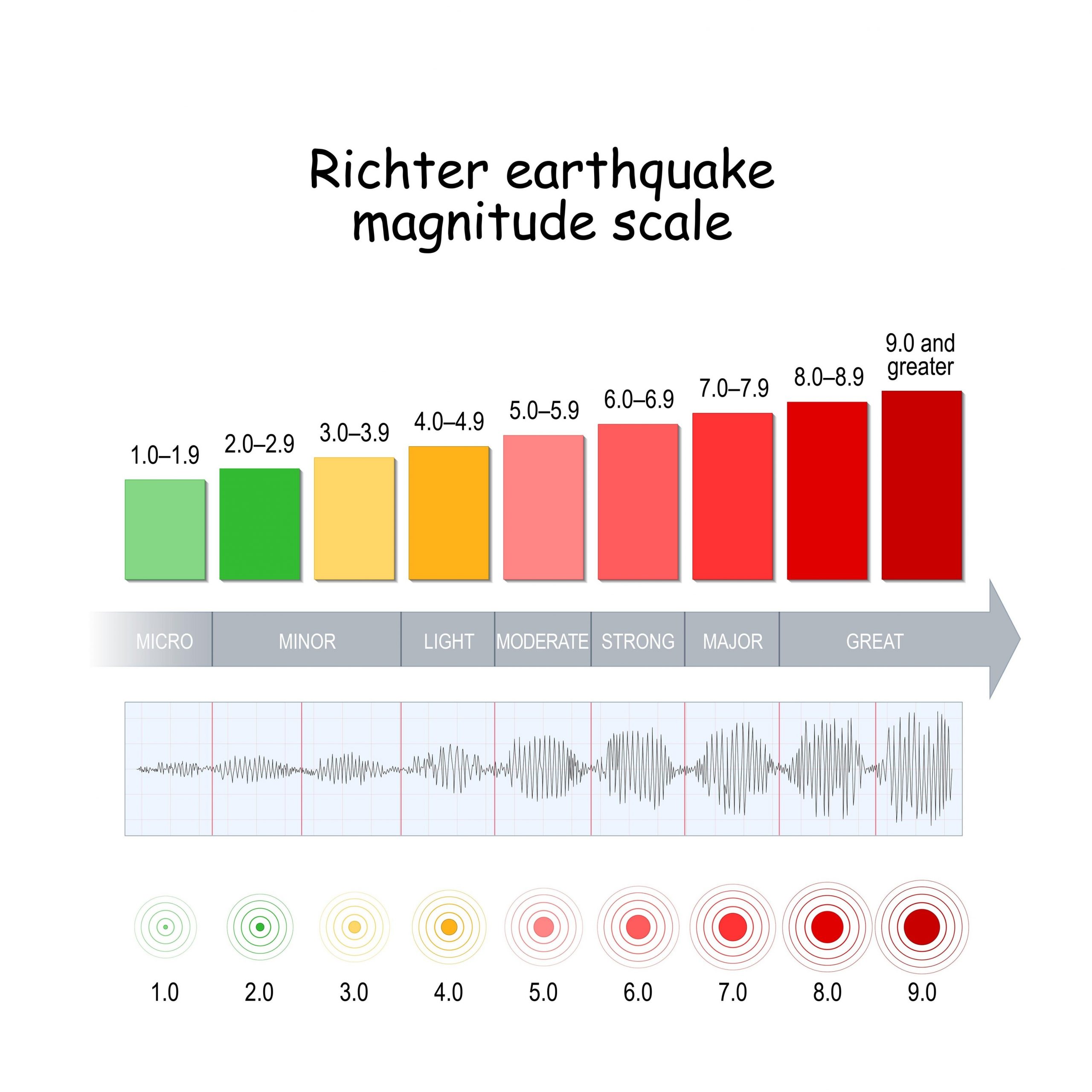
Dalam sains, kita sering berhadapan dengan angka yang sangat bervariasi, dari yang sangat kecil hingga sangat besar. Misalnya, intensitas gempa bumi, tingkat kebisingan, atau keasaman larutan (pH). Menggunakan logaritma memungkinkan kita untuk merepresentasikan rentang nilai yang luas ini dalam skala yang lebih mudah dikelola. Skala Richter untuk gempa bumi dan skala pH adalah contoh nyata dari penggunaan logaritma.

Licensed by Google

3. Solusi untuk Persamaan Eksponensial

Logaritma adalah kunci untuk memecahkan persamaan di mana variabel yang tidak diketahui berada di eksponen. Contohnya, jika kita ingin mencari tahu berapa lama waktu yang dibutuhkan agar sebuah populasi bakteri berlipat ganda, kita dapat menggunakan logaritma untuk menemukan jawabannya. Logaritma juga fundamental dalam kalkulus, terutama dalam memecahkan persamaan diferensial yang melibatkan pertumbuhan dan peluruhan eksponensial.

Properti Dasar dan Operasi Logaritma

Untuk dapat menggunakan logaritma secara efektif, kita perlu memahami beberapa properti dasar yang berlaku untuk semua jenis logaritma, selama basisnya positif dan tidak sama dengan 1. Properti-properti ini ibarat aturan main dalam permainan logaritma.

Properti Dasar Logaritma

Sifat Perkalian: Logaritma dari hasil perkalian dua bilangan adalah sama dengan penjumlahan logaritma dari masing-masing bilangan. $log_{b} (x y) = log_{b} (x) + log_{b} (y)$ Contoh: $log_{2} (8 \times 4) = log_{2} (8) + log_{2} (4) = 3 + 2 = 5$ . Karena $2^{5} = 32$ dan $8 \times 4 = 32$ , maka persamaan ini benar.
Sifat Pembagian: Logaritma dari hasil pembagian dua bilangan adalah sama dengan pengurangan logaritma dari masing-masing bilangan. $log_{b} (x / y) = log_{b} (x) - log_{b} (y)$ Contoh: $log_{3} (81/9) = log_{3} (81) - log_{3} (9) = 4 - 2 = 2$ . Karena $3^{2} = 9$ dan $81/9 = 9$ , maka persamaan ini benar.
Sifat Pangkat: Logaritma dari sebuah bilangan yang dipangkatkan adalah sama dengan pangkat tersebut dikalikan dengan logaritma dari bilangan aslinya. $log_{b} (x^{y}) = y log_{b} (x)$ Contoh: $log_{2} (4^{3}) = 3 log_{2} (4) = 3 \times 2 = 6$ . Karena $2^{6} = 64$ dan $4^{3} = 64$ , maka persamaan ini benar.
Sifat Pergantian Basis: Properti ini sangat berguna untuk mengubah logaritma dari satu basis ke basis lain, misalnya saat menggunakan kalkulator. $log_{b} (x) = l o g ^{c} ( b ) l o g ^{c} ( x )$ Contoh: Kita ingin mencari $log_{2} (8)$ . Kita bisa mengubahnya ke basis 10: $log_{2} (8) = l o g ^{10} ( 2 ) l o g ^{10} ( 8 )$ . Dengan kalkulator, kita akan mendapatkan $0.301 0.903 \approx 3$ .

Operasi Dasar Logaritma

Menghitung Logaritma: Untuk menghitung logaritma, kita perlu mencari tahu pangkat berapa yang diperlukan. Misalnya, untuk $log_{5} (25)$ , kita bertanya, “5 dipangkatkan berapa agar hasilnya 25?”. Jawabannya adalah 2. Jadi, $log_{5} (25) = 2$ .
Menggunakan Kalkulator: Hampir semua kalkulator memiliki tombol “log” (untuk basis 10) dan “ln” (untuk basis $e$ ). Untuk menghitung logaritma dengan basis lain, kita bisa menggunakan properti pergantian basis.

Logaritma dalam Kehidupan Nyata: Penerapan yang Luas

Meskipun terdengar seperti materi pelajaran yang hanya ada di buku, logaritma sebenarnya tersembunyi di banyak aspek kehidupan kita. Memahami penerapan ini dapat memberikan kita apresiasi yang lebih dalam terhadap pentingnya matematika.

1. Sains dan Teknologi

- Akustik: Skala desibel (dB) untuk mengukur intensitas suara adalah skala logaritmik. Peningkatan 10 dB berarti suara 10 kali lebih intens. Inilah mengapa suara yang kita dengar tidak terasa 10 kali lebih keras meskipun intensitasnya meningkat 10 kali lipat.

Licensed by Google

Kimia: Skala pH, yang mengukur keasaman atau kebasaan suatu larutan, juga merupakan skala logaritmik. Perubahan satu unit pH berarti perubahan konsentrasi ion hidrogen sebanyak 10 kali lipat.
Astronomi: Magnitudo bintang, yang mengukur kecerahan, adalah skala logaritmik. Bintang dengan magnitudo 1 lebih terang 100 kali dibandingkan bintang dengan magnitudo 6.
Geologi: Skala Richter, yang mengukur energi gempa bumi, adalah skala logaritmik. Setiap kenaikan satu poin pada skala Richter (misalnya, dari magnitudo 5 ke 6) menunjukkan gempa yang 10 kali lebih kuat.

2. Keuangan dan Ekonomi

Bunga Majemuk: Rumus bunga majemuk ( $A = P (1 + r)^{t}$ ) dapat diselesaikan menggunakan logaritma untuk mencari tahu berapa lama waktu yang dibutuhkan agar investasi tumbuh hingga jumlah tertentu.
Model Pertumbuhan: Para ekonom menggunakan model logaritmik untuk menganalisis pertumbuhan populasi, PDB, atau penyebaran teknologi.

3. Komputasi

Algoritma: Banyak algoritma dalam ilmu komputer, seperti pencarian biner, memiliki kompleksitas waktu logaritmik ( $O (log n)$ ). Ini berarti waktu yang dibutuhkan untuk menjalankan algoritma tidak tumbuh secepat ukuran input, membuatnya sangat efisien untuk data dalam jumlah besar.

Tantangan dan Kesalahan Umum dalam Belajar Logaritma

Seperti halnya materi matematika lainnya, ada beberapa tantangan yang sering dihadapi siswa saat mempelajari logaritma. Mengenali tantangan ini dapat membantumu menghadapinya dengan lebih baik.

Lupa Basis: Salah satu kesalahan paling umum adalah lupa mencatat basis logaritma. Ingat, $log (100)$ berbeda dengan $log_{2} (100)$ !
Salah Menggunakan Properti: Terkadang, siswa mencampuradukkan properti logaritma, misalnya mengira $log (x + y)$ sama dengan $log x + log y$ . Ingat, properti perkalian hanya berlaku untuk $log (x y)$ .
Anggapan Logaritma Sulit: Mindset bahwa logaritma adalah materi yang sulit seringkali menjadi penghalang terbesar. Padahal, dengan latihan dan pemahaman konsep yang benar, logaritma menjadi sangat mudah.

Kunci untuk menguasai logaritma adalah dengan banyak latihan soal. Mulailah dari soal-soal sederhana untuk memperkuat pemahaman konsep, lalu tingkatkan kesulitan secara bertahap. Jangan ragu untuk bertanya pada guru atau teman jika ada hal yang tidak kamu mengerti.

10 Soal Kuis untuk Menguji Pemahamanmu

Tuliskan bentuk eksponensial dari $log_{4} (64) = 3$ .
Berapakah nilai dari $log_{5} (125)$ ?
Sederhanakan ekspresi berikut: $log (5) + log (20)$ .
Jika $log_{a} (16) = 2$ , berapakah nilai $a$ ?
Selesaikan persamaan: $log_{3} (x) = 4$ .
Hitunglah nilai dari $log_{2} (8^{2})$ .
Ubah $log_{5} (100)$ ke dalam bentuk logaritma basis 10.
Sederhanakan ekspresi: $log_{7} (49) - log_{7} (7)$ .
Jika $log_{4} (x) = 3$ , berapakah nilai $x$ ?
Berapakah nilai dari $ln (e^{5})$ ?

Kesimpulan: Memanfaatkan Kekuatan Logaritma

Logaritma bukanlah sekadar bab dalam buku matematika, melainkan sebuah alat yang sangat powerful dengan jangkauan aplikasi yang luas. Dari menyederhanakan perhitungan yang rumit hingga membantu kita memahami fenomena alam dalam skala yang sangat besar, peran logaritma tak bisa diabaikan.

Dengan memahami konsep dasarnya, menguasai properti-propertinya, dan melihat bagaimana ia diterapkan dalam kehidupan nyata, kamu akan menyadari bahwa logaritma tidaklah semenakutkan yang kamu bayangkan. Ia adalah sebuah jembatan yang menghubungkan dunia eksponen dan matematika yang lebih tinggi. Jadi, janganlah takut untuk menjelajahinya. Selamat belajar!

Yuk, tingkatkan pemahamanmu tentang materi-materi pendidikan lainnya! Gabung sekarang di channel edukasi kami untuk mendapatkan informasi terbaru, tips belajar, dan materi eksklusif.

Bergabunglah dengan Channel WhatsApp (INFO Pendidikan) sekarang: https://whatsapp.com/channel/0029VaoZFfj1Hspp1XrPnP3q

Atau, gabung juga di Channel Telegram (INFO Pendidikan) kami: https://t.me/Infopendidikannew