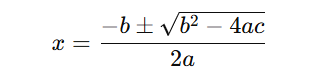Menyelami Dunia Aljabar: Memahami Persamaan dan Pertidaksamaan di Kelas 9

Aljabar adalah salah satu cabang matematika yang menjadi dasar penting dalam berbagai bidang ilmu. Mulai dari ilmu komputer, teknik, ekonomi, hingga bidang sosial, semuanya tak lepas dari konsep aljabar. Di kelas 9, pembelajaran aljabar semakin mendalam, terutama fokus pada persamaan dan pertidaksamaan.

Dalam artikel ini, kita akan mengupas tuntas apa itu aljabar, bagaimana cara menyelesaikan persamaan dan pertidaksamaan, serta mengapa keterampilan ini sangat penting dalam kehidupan sehari-hari. Mari kita mulai perjalanan ini!

Apa Itu Aljabar?

Secara sederhana, aljabar adalah cabang matematika yang menggunakan simbol dan huruf untuk mewakili angka dan bilangan. Konsep ini memungkinkan kita menyusun model matematika dari situasi nyata, memecahkan masalah, dan meramalkan hasil di masa depan.

Dalam aljabar, kita akan sering berhadapan dengan:

• Variabel, seperti $x$ dan $y$, yang merepresentasikan nilai yang tidak diketahui.

• Konstanta, yakni nilai tetap seperti angka 2, 5, atau -7.

• Operasi matematika seperti penjumlahan, pengurangan, perkalian, dan pembagian.

Konsep dasar ini menjadi pondasi untuk memahami topik-topik lebih kompleks, termasuk persamaan dan pertidaksamaan.

Persamaan: Menyusun dan Menyelesaikan

Persamaan dalam aljabar adalah pernyataan bahwa dua ekspresi memiliki nilai yang sama, biasanya ditandai dengan tanda sama dengan $=$. Di kelas 9, Anda akan mempelajari beberapa jenis persamaan, di antaranya:

1. Persamaan Linear

Persamaan linear adalah persamaan di mana variabel berpangkat satu. Bentuk umum persamaan linear satu variabel adalah:

​

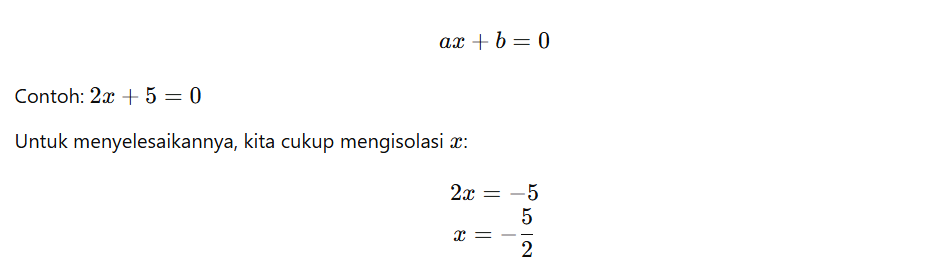
Persamaan linear juga bisa melibatkan dua variabel, seperti:

ax + by = c

Di mana kita memerlukan lebih dari satu persamaan untuk menemukan nilai x dan y.

2. Persamaan Kuadratik

Persamaan kuadratik adalah persamaan di mana variabel memiliki pangkat dua. Bentuk umumnya:

Cara umum menyelesaikan persamaan kuadratik antara lain:

• Faktorisasi

• Melengkapkan kuadrat

• Menggunakan rumus kuadratik:

​​

3. Persamaan Rasional

Persamaan rasional melibatkan pecahan yang variabelnya ada di penyebut. Contoh:

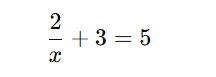
Langkah-langkah penyelesaiannya melibatkan:

• Menyamakan penyebut

• Menghilangkan pecahan dengan mengalikan kedua sisi dengan penyebut

• Menyelesaikan persamaan yang dihasilkan.

Penting untuk memeriksa solusi pada persamaan rasional karena bisa saja menghasilkan nilai yang menyebabkan pembagian dengan nol, yang tidak diperbolehkan.

Pertidaksamaan: Membuka Lebih Banyak Kemungkinan

Jika persamaan menyatakan kesamaan, maka pertidaksamaan menyatakan hubungan lebih besar, lebih kecil, lebih besar sama dengan, atau lebih kecil sama dengan.

Tanda pertidaksamaan yang umum digunakan:

• >(lebih besar dari)

• <(lebih kecil dari)

• ≥ (lebih besar atau sama dengan)

• ≤ (lebih kecil atau sama dengan)

1. Pertidaksamaan Linear

Pertidaksamaan linear satu variabel contohnya:

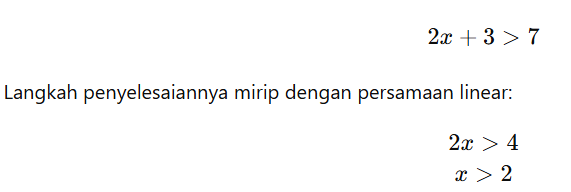
Solusi ini berarti semua nilai $x$ yang lebih besar dari 2 akan memenuhi pertidaksamaan tersebut.

Penting untuk diingat: jika kita mengalikan atau membagi pertidaksamaan dengan bilangan negatif, maka arah tanda pertidaksamaan harus dibalik.

2. Pertidaksamaan Kuadratik

Menyelesaikan pertidaksamaan kuadratik sedikit lebih rumit karena melibatkan mencari tanda positif atau negatif dari fungsi kuadrat.

Langkah-langkah umumnya:

1. Cari akar-akar persamaan kuadratik

2. Tentukan interval-interval berdasarkan akar tersebut.

3. Uji tanda fungsi kuadrat pada masing-masing interval.

3. Pertidaksamaan Rasional

Pertidaksamaan rasional adalah pertidaksamaan yang melibatkan pecahan dengan variabel di penyebut. Menyelesaikannya membutuhkan langkah ekstra:

• Menentukan nilai yang membuat penyebut nol (karena tidak boleh terjadi)

• Menyusun garis bilangan berdasarkan akar-akar dari pembilang dan penyebut

• Menentukan tanda pada setiap interval.

Menyelesaikan Sistem Persamaan dan Pertidaksamaan

Dalam beberapa soal, Anda akan menghadapi sistem persamaan atau pertidaksamaan, yang artinya lebih dari satu persamaan atau pertidaksamaan harus dipenuhi secara bersamaan.

Metode penyelesaian:

• Substitusi, mengganti satu variabel dari satu persamaan ke persamaan lain.

• Eliminasi, menjumlahkan atau mengurangkan dua persamaan untuk menghilangkan satu variabel.

• Grafik, menggambarkan masing-masing persamaan di bidang koordinat dan menemukan titik potong atau area irisan.

Sistem pertidaksamaan biasanya menghasilkan daerah solusi yang digambarkan sebagai area di bidang kartesius.

Mengapa Memahami Persamaan dan Pertidaksamaan Itu Penting?

Kemampuan memahami dan menyelesaikan persamaan dan pertidaksamaan adalah keterampilan yang sangat berguna, tidak hanya untuk ujian matematika, tetapi juga dalam kehidupan nyata.

Beberapa aplikasi nyata:

• Menghitung keuangan pribadi, seperti menentukan berapa banyak uang yang perlu ditabung untuk mencapai tujuan tertentu.

• Merencanakan bisnis, seperti menghitung biaya dan pendapatan untuk menentukan titik impas.

• Ilmu teknik, seperti menghitung kekuatan struktur bangunan.

• Ilmu komputer, seperti mengembangkan algoritma untuk memproses data.

Dengan memahami konsep ini, Anda menjadi lebih siap untuk menghadapi masalah logika dan analisis di berbagai bidang kehidupan.

Tips Belajar Aljabar Agar Lebih Mudah

Belajar aljabar bisa menjadi tantangan, tetapi dengan pendekatan yang tepat, siapa pun bisa menguasainya. Berikut beberapa tips:

1. Pahami konsep, jangan hanya menghafal rumus.

2. Latihan rutin dengan soal-soal beragam tingkat kesulitan.

3. Gunakan metode visual, seperti menggambar grafik, untuk memahami pola.

4. Belajar dari kesalahan, evaluasi setiap soal yang salah dan pahami mengapa jawaban tersebut salah.

5. Gunakan aplikasi pendukung seperti kalkulator grafik atau software pembelajaran untuk memperdalam pemahaman.

Kesimpulan

Memahami aljabar, khususnya persamaan dan pertidaksamaan, di kelas 9 bukan hanya penting untuk mencapai nilai akademik yang baik, tetapi juga membekali kita dengan keterampilan berpikir logis dan analitis yang diperlukan dalam kehidupan nyata. Dengan berlatih rutin, memahami konsep dasar, dan menggunakan strategi belajar yang tepat, Anda tidak hanya akan menguasai materi ini, tetapi juga siap menghadapi tantangan matematika di tingkat lebih lanjut.

Belajar aljabar bukan sekadar soal angka dan huruf—ini adalah langkah awal untuk membuka pintu menuju masa depan yang lebih cerah di bidang apa pun yang Anda pilih.