Mengenal Hubungan Trigonometri pada Segitiga Siku-Siku: Penjelasan Lengkap, Rumus, dan Contoh Soal – Trigonometri adalah salah satu cabang matematika yang kerap kali dianggap rumit oleh banyak pelajar. Namun, siapa sangka, kunci utama untuk memahami trigonometri justru dimulai dari sesuatu yang sangat sederhana: segitiga siku-siku. Dalam dunia geometri, segitiga ini punya peran besar, khususnya dalam membentuk dasar hubungan trigonometri seperti sinus (sin), cosinus (cos), dan tangen (tan).
Artikel ini akan membahas tuntas mengenai hubungan trigonometri pada segitiga siku-siku, rumus-rumus penting, hingga contoh soal yang mudah dipahami. Mari kita telusuri lebih dalam.
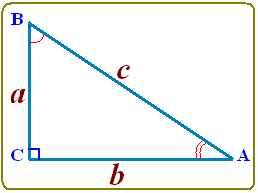
Apa Itu Segitiga Siku-Siku?
Sebelum melangkah ke trigonometri, penting untuk memahami apa itu segitiga siku-siku. Secara definisi, segitiga siku-siku adalah segitiga yang memiliki satu sudut tepat 90 derajat.
Dalam segitiga siku-siku, terdapat tiga sisi utama:
- Sisi Miring (Hipotenusa): Sisi yang paling panjang, berhadapan langsung dengan sudut 90°.
- Sisi Tegak: Sisi yang tegak lurus terhadap alas.
- Alas: Sisi yang menjadi dasar dari segitiga.
Mengapa Segitiga Siku-Siku Penting dalam Trigonometri?
Segitiga siku-siku menjadi dasar pengembangan trigonometri karena pada bentuk ini, hubungan antar sisi terhadap sudut bisa dihitung secara pasti. Melalui perbandingan antar sisi-sisi tersebut, kita bisa menentukan nilai sinus, cosinus, dan tangen suatu sudut.
Rumus Sin, Cos, dan Tan pada Segitiga Siku-Siku
Berikut adalah rumus dasar:
- Sinus (sin) = sisi depan sudut / sisi miring
- Cosinus (cos) = alas / sisi miring
- Tangen (tan) = sisi depan sudut / alas
Tabel Fungsi Trigonometri
| Fungsi Trigonometri | Rumus |
|---|---|
| Sinus (sin θ) | Sisi tegak / Sisi miring |
| Cosinus (cos θ) | Alas / Sisi miring |
| Tangen (tan θ) | Sisi tegak / Alas |
Contoh Soal Hubungan Trigonometri pada Segitiga Siku-Siku
Contoh Soal
Diketahui segitiga siku-siku ABC dengan:
- Sisi miring = 5 cm
- Sisi tegak = 4 cm
Hitunglah nilai sin A, cos A, dan tan A!
Penyelesaian
Menentukan alas menggunakan teorema Pythagoras:
Alas = √(5² – 4²) = √(25 – 16) = √9 = 3 cm
Maka diperoleh:
- Sin A = 4/5
- Cos A = 3/5
- Tan A = 4/3
Tabel Nilai Sin, Cos, dan Tan Sudut Istimewa
| Sudut | Sin | Cos | Tan |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | Tidak terdefinisi |
Aplikasi Hubungan Trigonometri dalam Kehidupan Nyata
- Arsitektur dan Konstruksi
- Navigasi Laut dan Udara
- Astronomi
- Teknologi GPS
Kesalahan Umum dalam Mempelajari Hubungan Trigonometri
- Keliru dalam menentukan sisi tegak dan alas
- Mengabaikan teorema Pythagoras
- Lupa membuat sketsa segitiga
- Salah menghitung pembagian
Tips Mudah Menghafal Rumus Trigonometri
- Gunakan singkatan SOH-CAH-TOA
- Buat ilustrasi berwarna
- Latihan soal setiap hari
Kesimpulan
Hubungan trigonometri pada segitiga siku-siku adalah fondasi penting dalam memahami banyak konsep matematika lanjutan. Dengan memahami rumus dasar sinus, cosinus, dan tangen, serta menerapkannya dalam berbagai soal, kita membangun pondasi yang kuat untuk menyelesaikan persoalan geometri, fisika, bahkan aplikasi teknologi modern.
Kunci utama dalam menguasai trigonometri adalah memahami konsep segitiga siku-siku, menghafal rumus, serta berlatih mengerjakan soal secara rutin. Jika dilakukan dengan konsisten, trigonometri akan terasa lebih mudah dan menyenangkan.