Hubungan Trigonometri pada Sudut Istimewa – Hubungan Trigonometri pada Sudut IstimewaDalam dunia matematika, khususnya pada bidang trigonometri, kita sering menjumpai yang disebut sebagai sudut istimewa. Sudut-sudut ini memiliki nilai trigonometri yang tetap dan sangat penting untuk dikuasai. Sudut istimewa tersebut adalah 0°, 30°, 45°, 60°, dan 90°. Menguasai nilai-nilai ini dapat membantu dalam menyelesaikan berbagai soal trigonometri dengan lebih cepat dan akurat.
Apa Itu Sudut Istimewa?
Sudut istimewa merupakan sudut dengan nilai tertentu yang sering digunakan dalam berbagai aplikasi matematika dan fisika. Tidak hanya dalam teori, dalam kehidupan sehari-hari pun nilai ini banyak digunakan, misalnya dalam bidang teknik, astronomi, dan navigasi. Menghafal nilai trigonometri untuk sudut-sudut ini adalah dasar penting dalam memahami konsep lebih lanjut dalam trigonometri.
Nilai Trigonometri untuk Sudut Istimewa
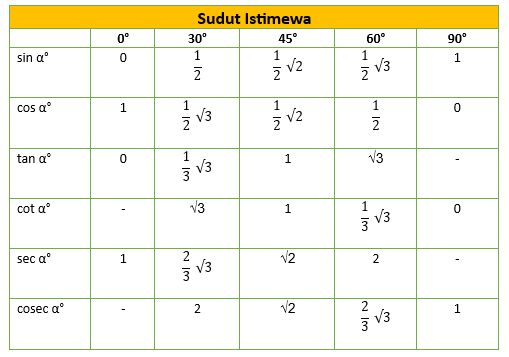
Berikut adalah tabel nilai sinus (sin), kosinus (cos), dan tangen (tan) untuk sudut-sudut istimewa:
| Sudut | Sin | Cos | Tan |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | Tidak Terdefinisi |
Pentingnya Menguasai Nilai Trigonometri Sudut Istimewa
Dalam banyak soal trigonometri, khususnya yang berkaitan dengan geometri, pemahaman terhadap nilai ini bisa mempercepat proses penyelesaian. Sebagai contoh, dalam menentukan tinggi suatu bangunan menggunakan konsep sudut elevasi, atau saat menghitung jarak antara dua titik dalam navigasi.
Penjabaran Rumus Hubungan Trigonometri
Hubungan antara sisi-sisi segitiga dan sudut-sudutnya dapat dijabarkan melalui rumus-rumus berikut:
- Sin θ = Sisi Depan / Sisi Miring
- Cos θ = Sisi Samping / Sisi Miring
- Tan θ = Sisi Depan / Sisi Samping
Dimana θ adalah sudut yang dimaksud dalam segitiga siku-siku.
Contoh Penerapan Hubungan Trigonometri pada Sudut Istimewa
Misalnya, dalam segitiga siku-siku, kita ingin mencari panjang sisi depan dengan sudut 30° dan sisi miring sepanjang 10 cm. Menggunakan rumus:
Sin 30° = 1/2
Maka:
Sisi Depan = Sin 30° × Sisi Miring = 1/2 × 10 = 5 cm
Bagaimana Cara Menghafalkan Nilai Trigonometri Sudut Istimewa?
Ada berbagai metode kreatif untuk menghafal nilai trigonometri ini, di antaranya:
- Menggunakan jari tangan dengan teknik “jari tangan trigonometri”
- Membuat tabel sederhana dan sering mengulang hafalan
- Memahami konsep dari asal-usul nilai tersebut, misalnya dari segitiga sama sisi dan segitiga siku-siku sama kaki
Kenapa Tan 90° Tidak Terdefinisi?
Salah satu hal menarik dalam tabel tersebut adalah nilai tan 90° yang tidak terdefinisi. Hal ini karena, dalam rumus tan θ = Sin θ / Cos θ, Cos 90° adalah 0, dan pembagian dengan nol dalam matematika dianggap tidak terdefinisi atau tidak bermakna.
Kesimpulan
Memahami hubungan trigonometri pada sudut istimewa merupakan bekal dasar yang sangat penting dalam pembelajaran matematika lanjutan. Dengan menguasai nilai-nilai trigonometri untuk sudut 0°, 30°, 45°, 60°, dan 90°, kita dapat lebih cepat dan efektif dalam menyelesaikan soal-soal trigonometri, baik dalam ujian maupun dalam penerapan nyata sehari-hari. Pemahaman mendalam terhadap konsep ini akan menjadi pondasi kuat untuk menguasai bidang matematika dan sains di tingkat yang lebih tinggi.